Chapter 3 Statistical Modeling
前一章的基本思路是已知这个数据符合某分布,在这个前提下,看出现特定值是否合理。但实际情况中不可能提供给研究者完美的符合某分布的数据,总是乱糟糟一团过来,然后看着分析去吧。如果要确定这个数据的统计学特征,需要从数据本身出发进行推断,这个过程即统计推论(statistical inference)。本章主要介绍这个过程。
原书中列出本章目标如下:
- 明确概率(probability)和统计(statistics)的区别。
- 应用直方图/矩形图/条形图(histograms),以及其他可视化工具,拟合数据到某分布。
- 通过数据模拟,使用极大似然率(maximum likehood)方法进行统计推论。
- 基于有预知信息的数据进行统计推论。这里将使用贝叶斯方法,引入新的特定分布。我们同样还会使用数据模拟,观察贝叶斯方法和极大似然率方法的差异。
- 使用统计模型和估测,计算(evaluate)二元分布和多元分布的依赖性。
- 分析一些历史上有趣的基因数据,数据以表格形式组织。
- 针对因变量数据(dependent data)应用马尔科夫链。
- 在基因组数据中做一些计数导向的练习,学习操作基因组数据的Bioconductor类型数据。
3.1 统计和概率模型的区别
前一章的统计模型,是已知数据所符合的分布,通过分布的参数,求出一个“事件(event)”的可能。如在表位一例中,已知数据符合 的泊松分布,然后可以求得发生次数大于等于7的事件概率为 。 这里泊松分布就是已知的原假设。

Figure 3.1: 已知分布,求某一事件概率
但实际上,得到的数据未必预先知道符合什么分布,比如有时你就是测出一堆蛋白或者基因序列来。这种时候,可能就需要倒过来计算,看看这些数据符合什么分布(概率模型 F),并求得分布模型的参数,这个过程就是统计推论。
3.2 一个简单的统计建模
建模首先要看数据符合什么分布。分布有很多,二项分布、多项分布、泊松分布,这是对离散变量的,正态分布、指数分布等,是针对连续变量的。有时候变量过于复杂,一种分布难以涵盖其特点,也会用混合模型来拟合,这个第四章会讲到。
还是看上一章用过的表位数据,这次假设提前不知道分布。并且先把极值去掉。
## e99
## 0 1 2
## 58 34 7
要看数据是否符合某分布,原书介绍了一种拟合优度检验图(goodness-of-fit diagram)的方法,叫他娘的什么根图(rootogram),这方法是2016年提出来的,还没有经过时间的历练,而且是否符合分布这样的工作,实际工作中很少遇到,稍微看看就行了。
library("vcd") # 需要这个包。
gf1 = goodfit(e99, "poisson") # goodfit这个函数,拟合数据。
rootogram(gf1) # rootogram作图,红点是理论分布所在的位置,然后把实际数上提或者下压。
越符合分布,差别的越小。看来这99个数提的压的都不多,还算符合泊松分布,下一步就是估计分布的参数,这里就是。
估计的方法就是通过数据计算最接近的,这叫极大似然估计(maximum likelihood estimator, MLE)。当然可以通过一系列 rpois(100, 1)、rpois(100, 2)、rpois(100, 3)。。。来看到底哪个更符合,但首先这样工作量很大,其次的值可以是小数,不一定试多少次,实际通过数学变换可以做的更优雅一点。
计算当泊松分布时,见到e100这个数据的概率。
当 时,。利用向量计算特性,可以这样计算:
## [1] 1.392143e-110这个可能性就叫的似然函数(likelihood function),公式写作,注意这个连乘符号,其公式写法和连加符号基本一致:
鉴于里面连乘的数都太小,取log后再计算会比较容易,对手算和电脑都是如此。当log后,m满足这个公式取值最大的时候,m就是。 可以按如下方式进行模拟。
loglikelihood = function(lambda, data = e100) {
sum(log(dpois(data, lambda)))
}
lambdas = seq(0.05, 0.95, length = 100)
loglik = vapply(lambdas, loglikelihood, numeric(1)) #后面这个numeric(1)是对返回结果的控制,就要1个数字,其实这里没必要,因为loglikelihood只返回一个数字,但作为参数必须写上。
plot(lambdas, loglik, type = "l", col = "red", ylab = "", lwd = 2,
xlab = expression(lambda))
m0 = mean(e100) # 为啥平均值就是要找的点?
abline(v = m0, col = "blue", lwd = 2)
abline(h = loglikelihood(m0), col = "purple", lwd = 2)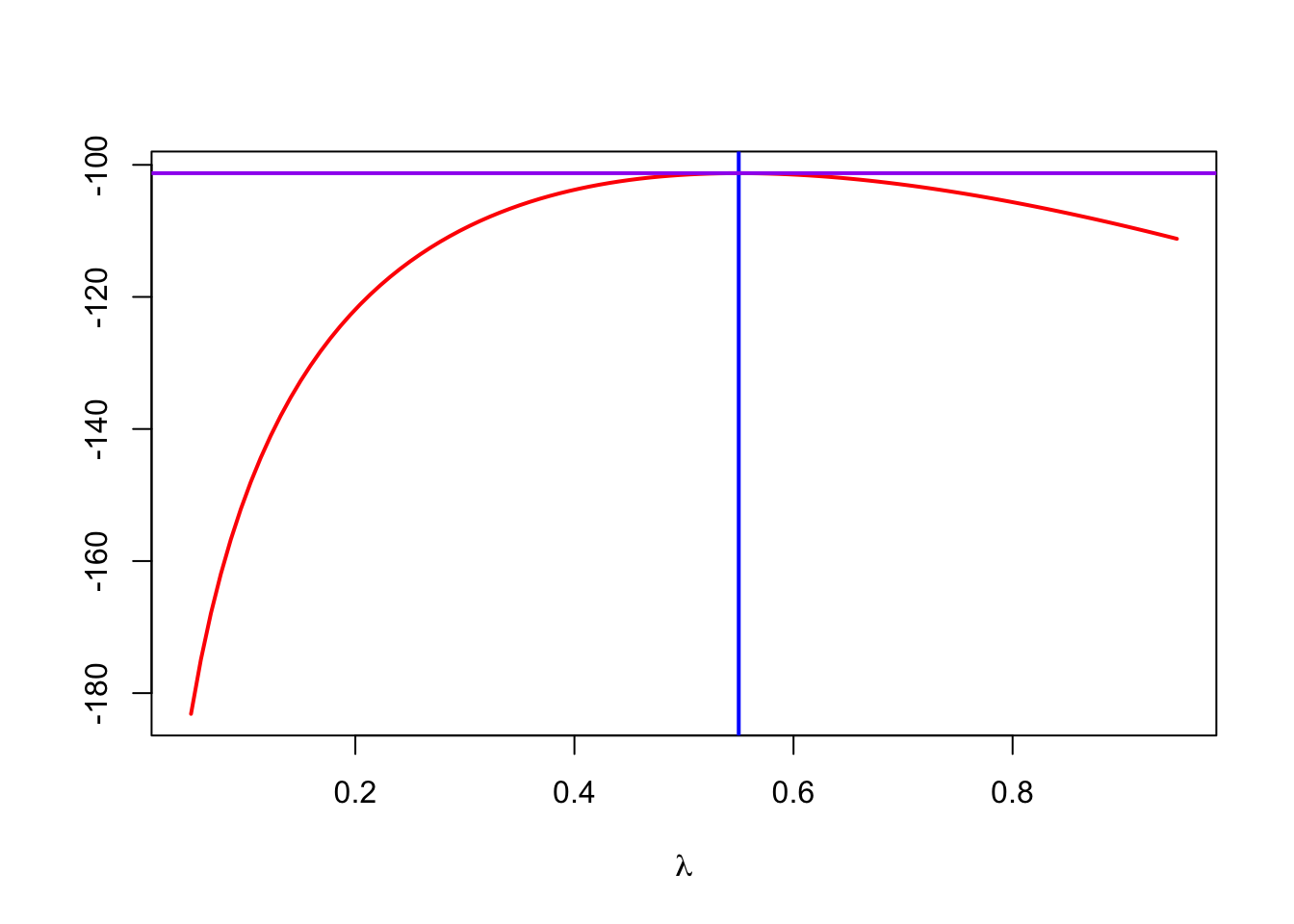
## [1] 0.55实际上使用vcd包里的goodfit函数,也能计算出来,轮子已经制造好了。
## [1] "observed" "count" "fitted" "type" "method" "df"
## [7] "par"## $lambda
## [1] 0.55如果使用0.55 重新做上一章的表位检测例题,还是有些不同的。
| 频率 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 按0.5 | 9 | 23254 | 60529 | 14528 | 1531 | 141 | 8 | 0 | 0 |
| 按0.55 | 3 | 15416 | 62606 | 19239 | 2508 | 209 | 17 | 1 | 1 |
下面解释前面的疑惑:为什么mean(e100)能使似然率最大?
要求得能使上面函数取最大值的,我们对 求导(derivative),使之成为0。
由此求得,当 的时候,函数取值最大。这一段是已知分布,推断参数,还有一类问题是求那种分布最合适,属于拟合优度(goodness of fit)的问题,后面会涉及。
3.2.1 这就是经典数据的经典统计?
经典统计检验框架下,只考虑一个模型,称数据的原假设(null model)。这种只考虑一个模型的原假设,不管具体数据出自哪个处理,哪个组别,统统认为是出自同一分布的随机数据。这样一来,分析者只能跟检验这些数是否真的出自这个模型、按这个模型出现这些数的概率有多少之类的问题较劲,没有别的分析方向。如果符合一个模型了,比如泊松分布,我们就能知道出现某个异常值的概率到底是多小。
3.2.2 讲到了一点回归分析
对一般的连续变量回归模型 , 要求a和b,残差(residuals)e的要符合正态分布,还能估算这个分布的变异(variance)。
对离散变量(count data),也可以应用回归模型,但残差分布不是正态的,需要应用广义线性模型(generalized linear models)。第八章、第九章中分别对RNA序列、下一代测序数据和16SrRNA数据应用该分析。
3.3 二元分布和极大似然率
遇到的二元分布实际数据经常是n个事件(trials),结果已知但不知道成功概率是多少,要去估算。比如知道扔了120次硬币,10次正面朝上,则可以估计概率。也可以按概率从小到大挨个试试。
probs = seq(0, 0.3, by = 0.005) # 从0到0.3,每0.005一个。
likelihood = dbinom(10, prob = probs, size = 120)
plot(probs, likelihood, pch = 16, xlab = "probability of success",
ylab = "likelihood", cex=0.6)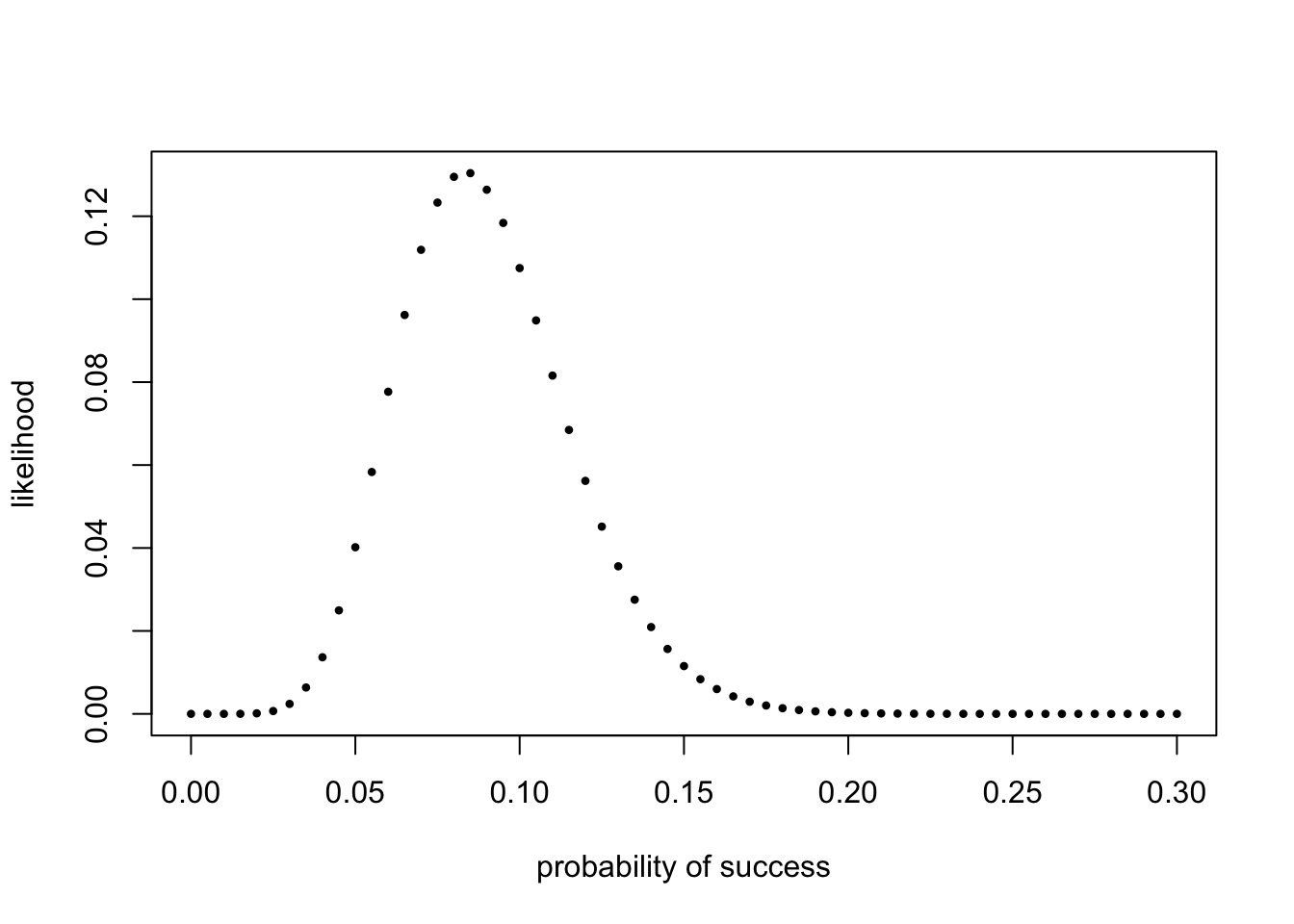
## [1] 0.085差球不多,在0.005精度下,是最接近的了。不明白为啥要这么搞一遍,可能为了让更加熟悉函数吧。
3.3.1 可能性就是概率,概率就是可能性的概率
一方面,在给定参数的条件下,概率分布能告诉我们见到特定数据的可能性是多少;另一方面,当数据确定时,我们去寻求最可能出现这些数据的分布。
如300次观测,40次成功。按排列组合计算,
两边log后,得:
按这个做个函数,然后作图。
loglikelihood = function(theta, n = 300, k = 40) {
115 + k * log(theta) + (n - k) * log(1 - theta)
}
thetas = seq(0, 1, by = 0.001) # 一串串概率试一试
plot(thetas, loglikelihood(thetas), xlab = expression(theta),
ylab = expression(paste("log f(", theta, " | y)")),type = "l")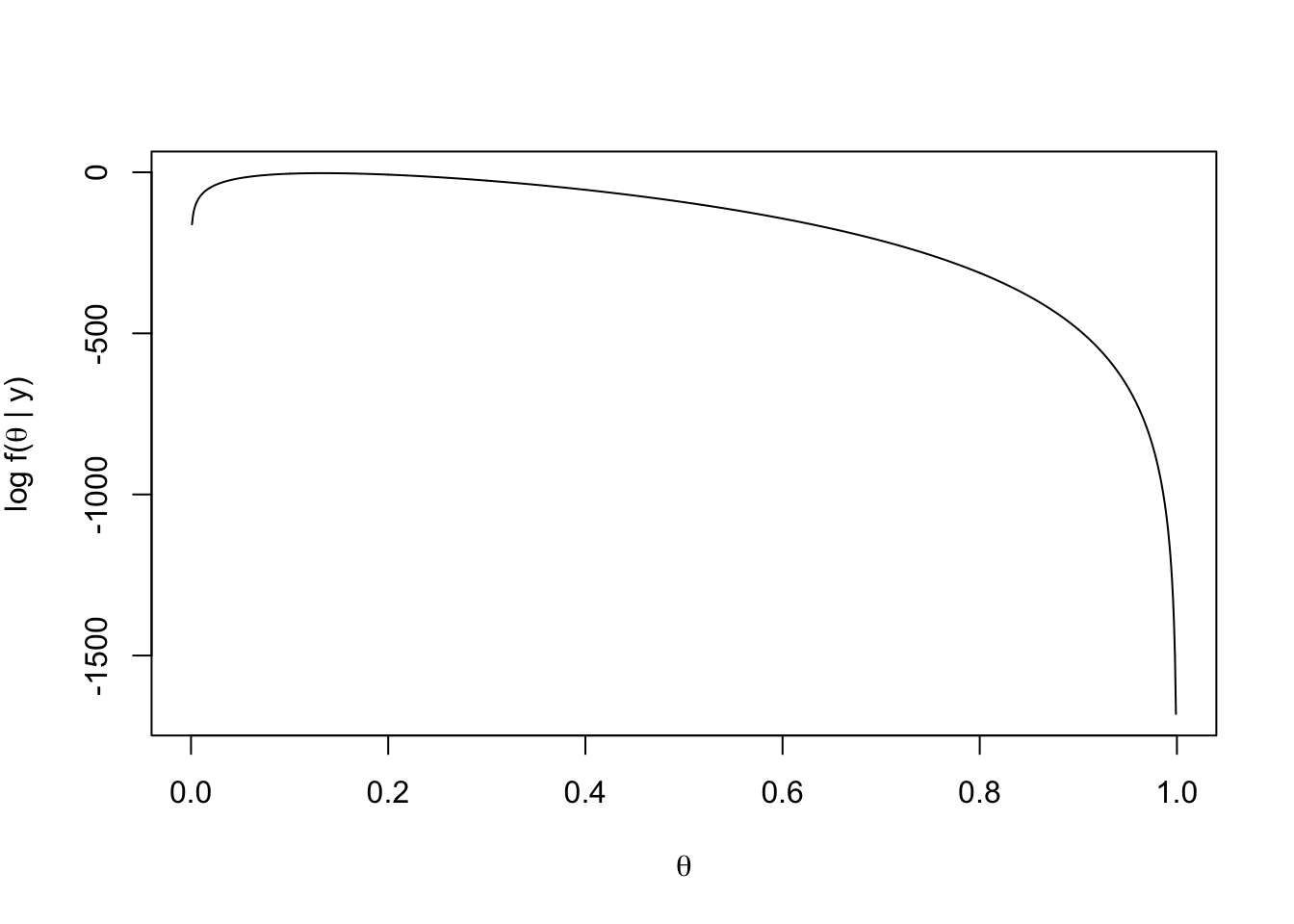
发现虽然40/300=0.13333最合适,但还有一段一直到0.2左右,都能出现最大可能。这一特性将会在后面的贝叶斯方法中见到。
3.4 多元数据
对DNA的组成,AG嘌呤,CT嘧啶,四种碱基构成多元数据。这里用Bioconductor包的函数,读取一段真正的DNA序列,是金黄葡萄球菌(Staphylococcus aureus)的fasta格式数据。
安装需要这样:
if (!requireNamespace(“BiocManager”, quietly = TRUE)) install.packages(“BiocManager”)
BiocManager::install(“Biostrings”)
折腾了这么久,终于见到真的数据了。。。可以看看数据结构,是2650条DNA序列,主体是一串串的ATGC字母,有名字,有宽度。可以用函数看看各碱基出现频率。
## A T G C
## 522 392 229 219为什么用[[]],不用[]?因为[[]]表示的火车这节车厢里面的货物,[]表示的是这节车厢。
然后进入有意义的问题——通过对比前十个基因的碱基出现频率是否一致,来推断其遗传特征是否相同。
letterFrq = vapply(staph, letterFrequency, FUN.VALUE = numeric(4),
letters = "ATGC", OR = 0) # 计算各基因碱基频率,并处理好从哪个基因出来的。
colnames(letterFrq) = paste0("gene", seq(along = staph)) # 4行、2650列,一列是一个基因。
letterFrq[,1:10] #查看下前10列## gene1 gene2 gene3 gene4 gene5 gene6 gene7 gene8 gene9 gene10
## A 522 413 85 411 685 887 275 510 487 191
## T 392 352 74 327 531 793 250 445 357 252
## G 229 193 56 207 423 586 169 316 263 142
## C 219 176 31 168 293 395 137 244 180 111tab10 = letterFrq[, 1:10] # 这就是前10个基因,ATGC各有多少个
computeProportions = function(x) {x/sum(x)} # 构造个函数,大概为了下一步好用apply。
prop10 = apply(tab10, 2, computeProportions) # 对列计算比例,即对每个基因计算碱基比例。
round(prop10, digits = 2) # 取两位小数## gene1 gene2 gene3 gene4 gene5 gene6 gene7 gene8 gene9 gene10
## A 0.38 0.36 0.35 0.37 0.35 0.33 0.33 0.34 0.38 0.27
## T 0.29 0.31 0.30 0.29 0.27 0.30 0.30 0.29 0.28 0.36
## G 0.17 0.17 0.23 0.19 0.22 0.22 0.20 0.21 0.20 0.20
## C 0.16 0.16 0.13 0.15 0.15 0.15 0.16 0.16 0.14 0.16## A T G C
## 0.3470531 0.2999714 0.2011442 0.1518313后面又通过蒙特卡洛检验这10个基因碱基含量的合理性。略。
3.5 卡方分布 ()
基本统计,卡方检验可以替代复杂的模拟,介绍了一些应用。
3.6 查格夫定律(Chargaff’s Rul)
来自任何生物体的任何细胞的DNA应该具有1:1的嘧啶和嘌呤碱基比例,更具体地说,鸟嘌呤的量应该等于胞嘧啶,并且腺嘌呤的量应该等于胸腺嘧啶。这种模式存在于DNA的两条链中。它们是由奥地利出生的化学家Erwin Chargaff 在20世纪40年代后期发现提出的。
## A T C G
## Human-Thymus 30.9 29.4 19.9 19.8
## Mycobac.Tuber 15.1 14.6 34.9 35.4
## Chicken-Eryth. 28.8 29.2 20.5 21.5
## Sheep-liver 29.3 29.3 20.5 20.7
## Sea Urchin 32.8 32.1 17.7 17.3
## Wheat 27.3 27.1 22.7 22.8
## Yeast 31.3 32.9 18.7 17.1
## E.coli 24.7 23.6 26.0 25.73.7 贝叶斯方法
待续。。。