Chapter 2 Generative Models for Discrete Data 广义模型和离散数据
2.1 本章概述
这一章从介绍概率、不同分布开始,假设各种符合某分布的数据,主要以DNA、碱基等为描述对象。原书中的说法是 top-bottom 的方式,从我们了解的各种概率分布(top)开始,设计符合这些分布原则的具体问题,如碱基分布模式等。当然这是一种理想化的训练,实际的问题多是反方向 bottom-top 的,通过分析实际数据获取数据规律,或者建立模型。
本章主要目标包括:
获取特定模型下所有可能结果的概率,并将理论值与实际数据比较。 Learn how to obtain the probabilities of all possible outcomes from a given model and see how we can compare the theoretical frequencies with those observed in real data.
通过一个完整示例,了解如何应用泊松分布分析抗原数据。
Explore a complete example of how to use the Poisson distribution to analyse data on epitope detection.如何应用泊松分布、二项式分布、多项式分布模型来做实验。
See how we can experiment with the most useful generative models for discrete data: Poisson, binomial, multinomial.使用R函数计算概率和偶发事件。
Use the R functions for computing probabilities and counting rare events.生成符合特定分布的随机数。
Generate random numbers from specified distributions.
有一点比较疑惑 —— 统计理论可以藏得多深?这里找的一些例子和统计分布关系密切,但之前一些相关、回归、降维的分析,基本涉及不到统计分布的知识。希望通过学习能把这些之间的内在联系搞清楚一点。
2.2 回顾一点概率论与数理统计
看这一章,感觉有些概念不清楚,再去学陈希孺老先生的的《概率论与统计统计》。

Figure 2.1: 陈希孺老先生的概率论与数理统计
带着点问题重新硬着头皮读,才发现这真的如同很多牛人推荐的,是一本神仙书。原来读的时候太功利,总想翻上几页就能拿去在R语言上套函数解决实际问题了,可看了看都是理论性的东西用不上,就丢到一边。现在再看,才发现老先生真是不紧不慢、娓娓道来,从“道”的高度把概率论和数理统计的有关概念、发展历程、应用场景等等系统的解释一遍。虽然是入门书,但好多领域的拓展也有谈及,用平实的语言勾画了宏大的场景,让人越读越有跪感。
| 名词 | 定义 | 原书涉及 |
|---|---|---|
| 试验/Trial | 要有明确界限,宽泛的可以包含“观察”。全部结果是试验前即明确的,如抛硬币2面,掷骰子6点,事件发生概率为0到正无穷。 | Tossing a coin has two possible outcomes. This simple experiment, called a Bernoulli trial, is modeled using a so-called Bernoulli random variable. |
| 事件/envent | 一个明确的陈述,界定了试验全部可能结果中一确定的部分,这个陈述或这一确定的部分,即一个事件。 | In molecular biology, many situations involve counting events. |
古典概率计算归结为计算两个数M和N,这种计算多涉及排列组合。如n个不同物体,取r个的排列数是 ,而不同组合数则为 ,这个 又称为组合系数,统计上习惯用这种形式来表示:。
组合系数 又常称为二项式系数,因为常出现在下列二项式展开的公式中: 还有多项式系数,n个相异物分成k堆,各堆个数分别为分法是。 它是的展开式中,这一项的系数。
不知道这几个公式和二项分布、多项分布有啥关系……不过老先生不会随便说,放着慢慢领会。
感觉清楚点了抓紧回过头看本书。概率论与数理统计晚点再学。
2.3 生命科学一些基础知识(直接看图)
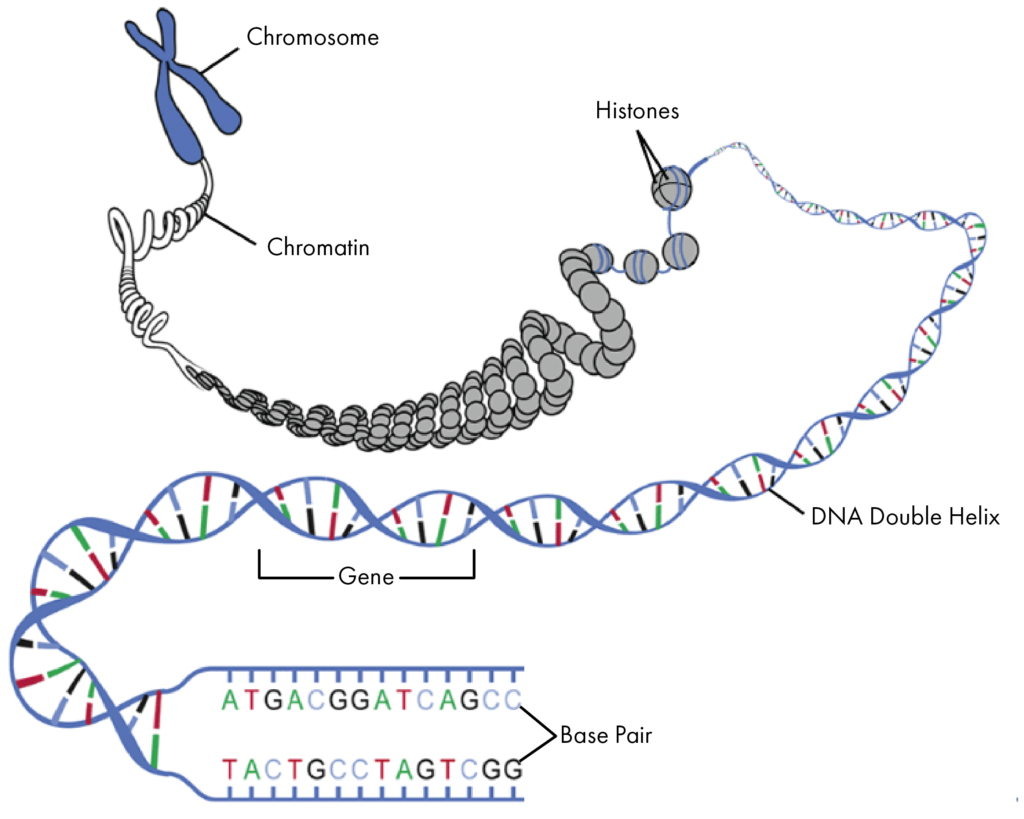
Figure 2.2: DNA 展开结构示意图。染色体-染色质-组织蛋白-脱氧核糖核酸双螺旋结构-基因-碱基对
,“how many codons use a certain spelling”](static/Users/eco/M%20for%20M/01-generative_files/codon.jpg)
Figure 2.3: RNA上的密码子codons,“how many codons use a certain spelling”
2.4 本章大体框架
如原文所说,这一章是一种“从上而下”的套路练习。通过设计一些符合概率分布模型的数据,了解数据和概率之间的关系。主要讲了4种分布:
伯努利分布(Bernoulli distribution),是二项式分布的特殊形式(n = 1)又称两点分布或者’0-1’分布,要么成功是1,要么失败是0,只有一种可能。
二项式分布(binomial distribution),二项分布即重复n次的伯努里试验,典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。按陈先生的思路,这就是一个排列组合问题:要在扔n次中有k次成功,成功概率为p,则失败概率为1-p,每次试验独立,则要求k个p都要发生,n-k个1-p也要发生,即 。如果不明白的话考虑一下扔硬币,正面想上的概率是0.5,扔两次正面都往上的概率是,扔四次,两次正,两次反的概率是。再回到n次,有k次成功,发生的位置,或者说次序可能不同,占据k个位置有 种可能,所以发生k次成功的几率为:。这个分布和泊松分布、正态分布都有联系。n很大而p很小时,n*p趋近一个常数,就近似为泊松分 布(这个在手动计算的年代方便、好算),这两种都是离散分布。
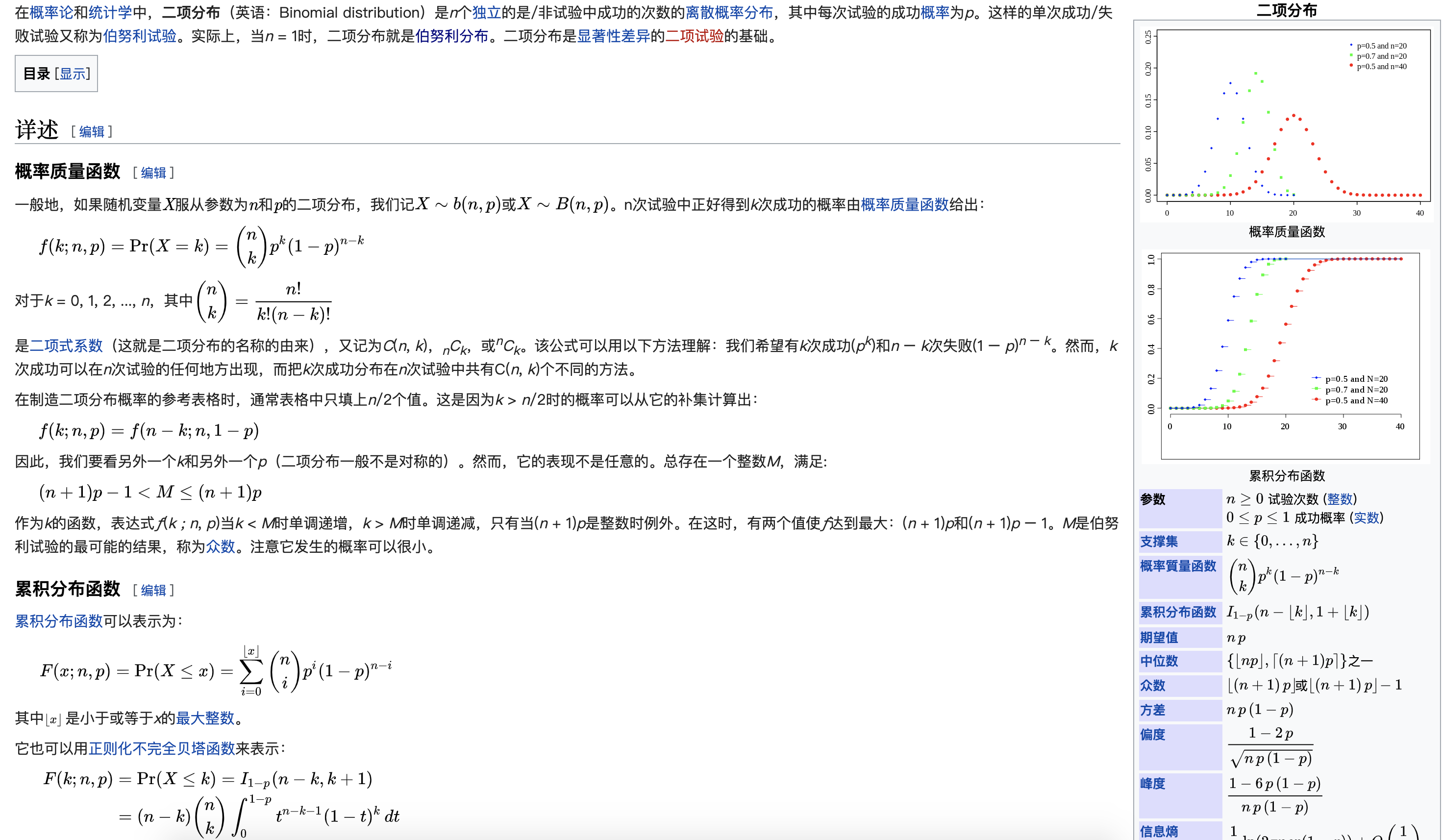
Figure 2.5: 二项分布的维基百科解释
- 泊松分布(Poisson distribution),泊松分布是二项分布n很大而p很小时的一种极限形式。
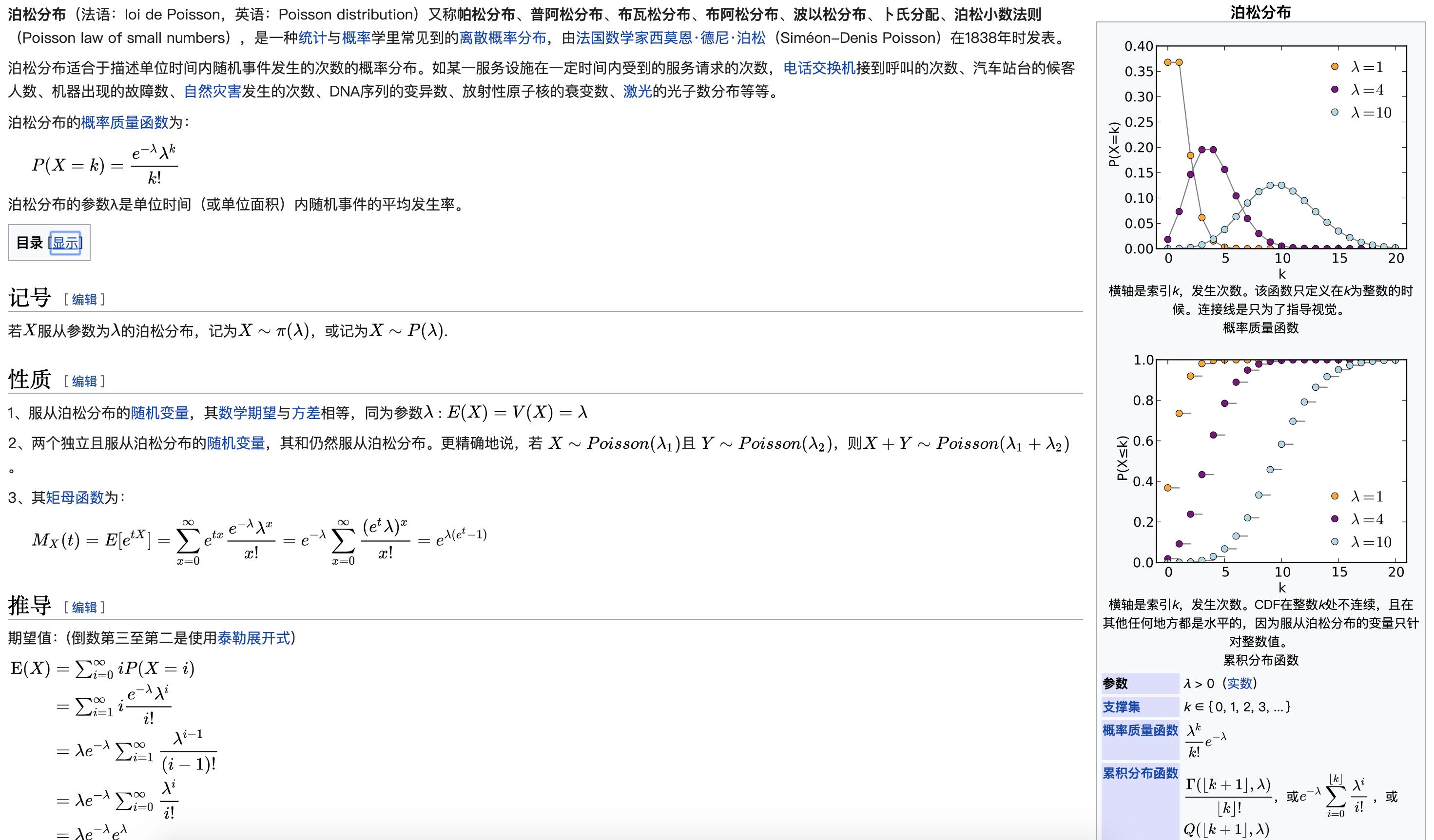
Figure 2.6: 泊松分布的维基百科解释
- 多项分布(multinomial distribution)二项扩展为多项就得到了多项分布。二项分布的试验结果只有两个(成功和失败),而多项分布的试验结果则多于两个。如果试验的结果有三个,则是三项分布;如果结果有六个,则是六项分布比如扔骰子,不同于扔硬币,骰子有6个面对应6个不同的点数,这样单次每个点数朝上的概率都是1/6(对应p1~p6,它们的值不一定都是1/6,只要和为1且互斥即可
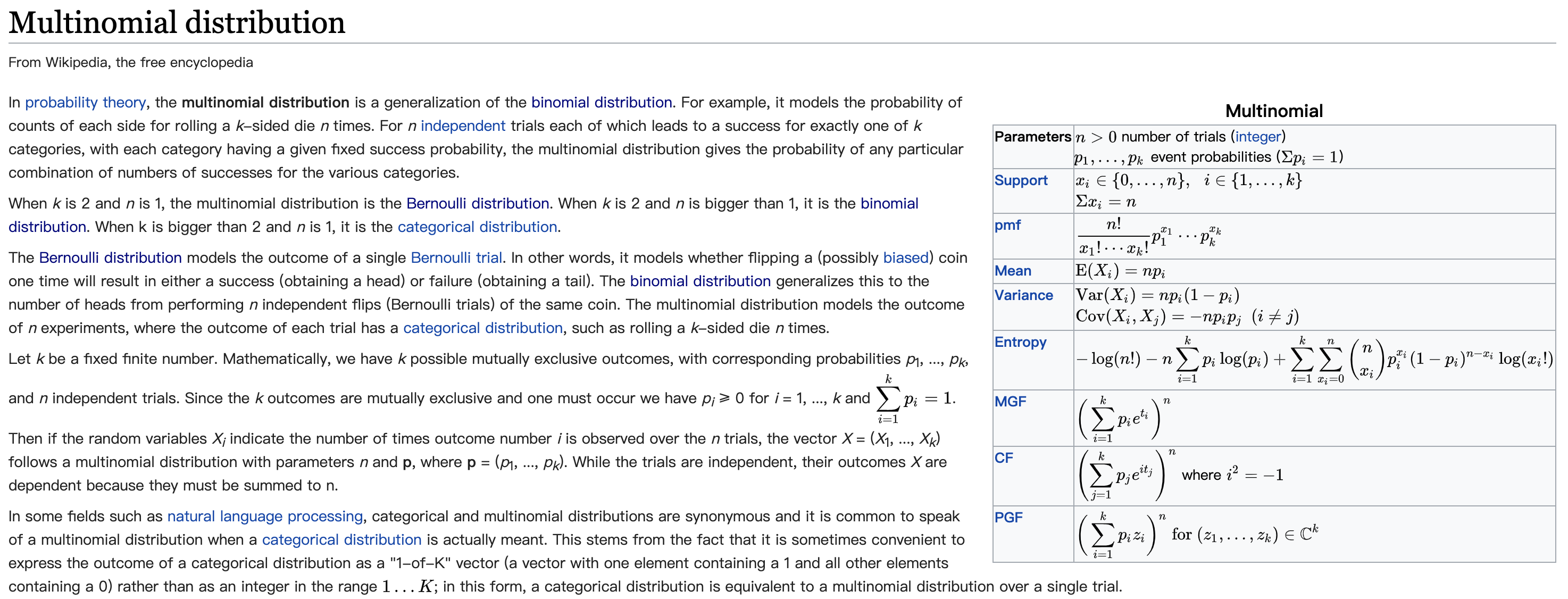
Figure 2.7: 多项式分布的wikipedia解释
2.5 泊松分布
原书首先介绍了泊松分布的一个示例。在一段HIV基因上,一次转录发生突变的概率为, 也就是说,一段含有10000个核苷酸(nucleotides)的HIV基因,在一次复制过程中,发生突变的核苷酸个数在5左右,标准差为。这个5,在R语言的泊松分布公式中,称为频率参数(rate parameter),写作。 通过确定了出现频率的泊松分布,可以计算某个频率出现的概率。如,计算这段DNA中出现3个变异的概率是多少,实现方式如下。
## [1] 0.1403739本来不太明白,R里面说lambda是平均数(vector of (non-negative) means.),这里是5,可能没有明确在10000里面发生5啊,那么dpois(x = 30, lambda = 50) 应该得到一样的值吧,可实际上差大了。why!
其实呢,这个5,其实是单位时间的平均发生率。如同“一段时间内某路口发生事故的个数”一样,其实就是n*p。。上面R的函数中,是知道是5,求发生3次的可能是多少。
结合R中的作图,和非常牛逼非常适合统计的向量数据处理方式,可以把泊松分布画出来。能够清晰地看到,是5的时候,发生0到12次的概率分别是多少。
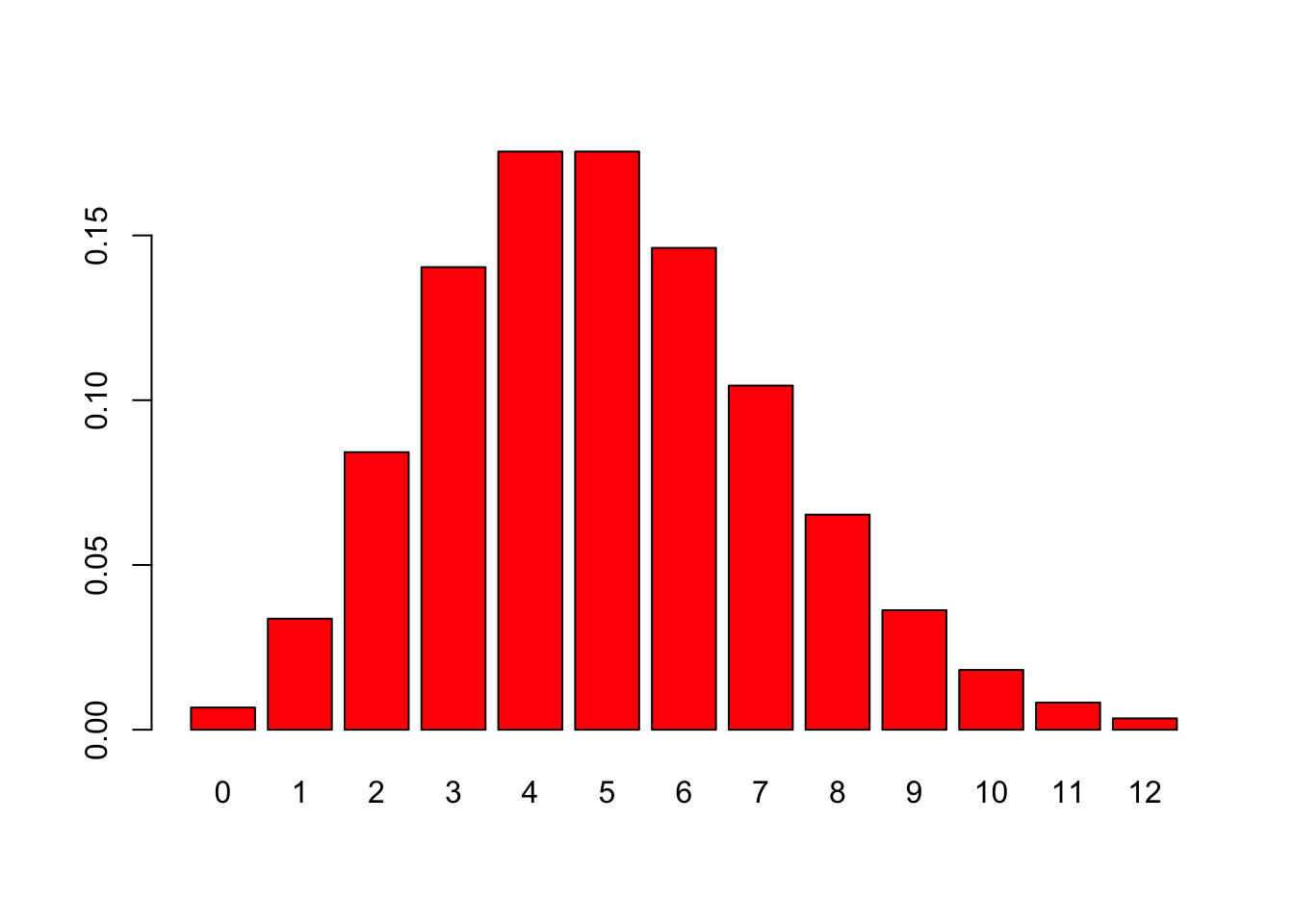
Figure 2.8: 发生1到12次突变的概率分布
2.6 荡开一会看R语言的函数
在R语言中,一个概率一般有4种不同的函数,如泊松分布是这样的。
- Density, distribution function, quantile function and random generation for the Poisson distribution with parameter lambda.
| 函数 | 名称 |
|---|---|
| dpois(x, lambda, log = FALSE) | 密度函数 |
| ppois(q, lambda, lower.tail = TRUE, log.p = FALSE) | 分布函数 |
| qpois(p, lambda, lower.tail = TRUE, log.p = FALSE) | 分位数函数 |
| rpois(n, lambda) | 随机数生成函数 |
| 参数 | 意义 |
|---|---|
| x | vector of (non-negative integer) quantiles. |
| q | vector of quantiles. |
| p | vector of probabilities. |
| n | number of random values to return. |
| lambda | vector of (non-negative) means. |
| log, log.p | logical; if TRUE, probabilities p are given as log(p). |
| lower.tail | logical; if TRUE (default), probabilities are P[X ≤ x], otherwise, P[X > x]. |
里面的 quantiles, 分位数,拿出来说一下,也叫分位点,就是概率分布上选的点,常用的有中位数、四分位数、十分位数、百分位数等。感觉是原来手工时代的习惯,在函数中只要是整数,往上放就行,如前面例子中用的3。就是这段基因发生突变的平均数为5,那发生3次突变的概率是多少。3怎么分位了?我要高兴随便写个100也行,就是概率小点而已。可以理解为成功次数。为什么叫density,就是因为只看这一次的,是密度。对应的是massive,质量,在R里面是distribution function, 如二项分布里的pbinom,就是这个次数之前累积的了。
二项分布
## [1] 0.2460938## [1] 0.6230469## [1] 0.6220703## [1] 0.3769531再看看泊松分布,也类似。
## [1] 0.1403739## [1] 0.2650259## [1] 0.2650259## [1] 3另外可以方便地生成符合分布的随机数。
## [1] 0 1 0 1 1 1 1 1 1 1 0 1 0 0 0## [1] 112.7 应用一个表位检测模型(a generative model for epitope detection)
有的蛋白会引发人体过敏(allergic reaction),蛋白大分子上引发过敏的位置叫表位(epitope)。面对抗原(antigen),白细胞会产生抗体(antibody)。有些抗体直接摧毁抗原,有些召集(recruit)白细胞摧毁抗原。表位是免疫系统识别抗原的关键位置,如抗体、B细胞、T细胞,大多通过表位识别抗原。

Figure 2.9: 抗体示意图,不同颜色是免疫球蛋白
基于上述,看这个 ELISA error model,即酶联免疫吸附试验,用来检测某蛋白不同位置的特定表位。该模型有以下假定: > * 一般人都能检测出敏感表位,叫噪声值,检测到的概率为0.01,检测到表位标记为1.
- 在100个不同位置检测某蛋白,检测相对独立。
- 本章检测50个病人的样本。
先做个符合设定的一个病人的分布。
## [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [36] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [71] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0如果每个病人的过敏表位都泊松分布的,那么50个病人的数据加起来,数据也应该符合泊松分布,只不过检测到的概率成了0.01*50=0.5,类似下面这样的分布。
## [1] 0 1 0 0 0 0 0 0 0 1 2 0 0 1 0 1 0 0 0 1 0 1 1 0 0 0 1 1 0 2 2 1 1 0 1
## [36] 0 0 1 0 0 0 0 1 1 0 0 0 1 1 1 3 0 0 0 0 1 2 0 2 0 2 0 0 1 0 0 2 1 0 2
## [71] 1 1 0 1 0 0 1 0 0 1 0 2 0 0 0 3 1 1 1 0 0 1 0 0 1 0 0 1 0 1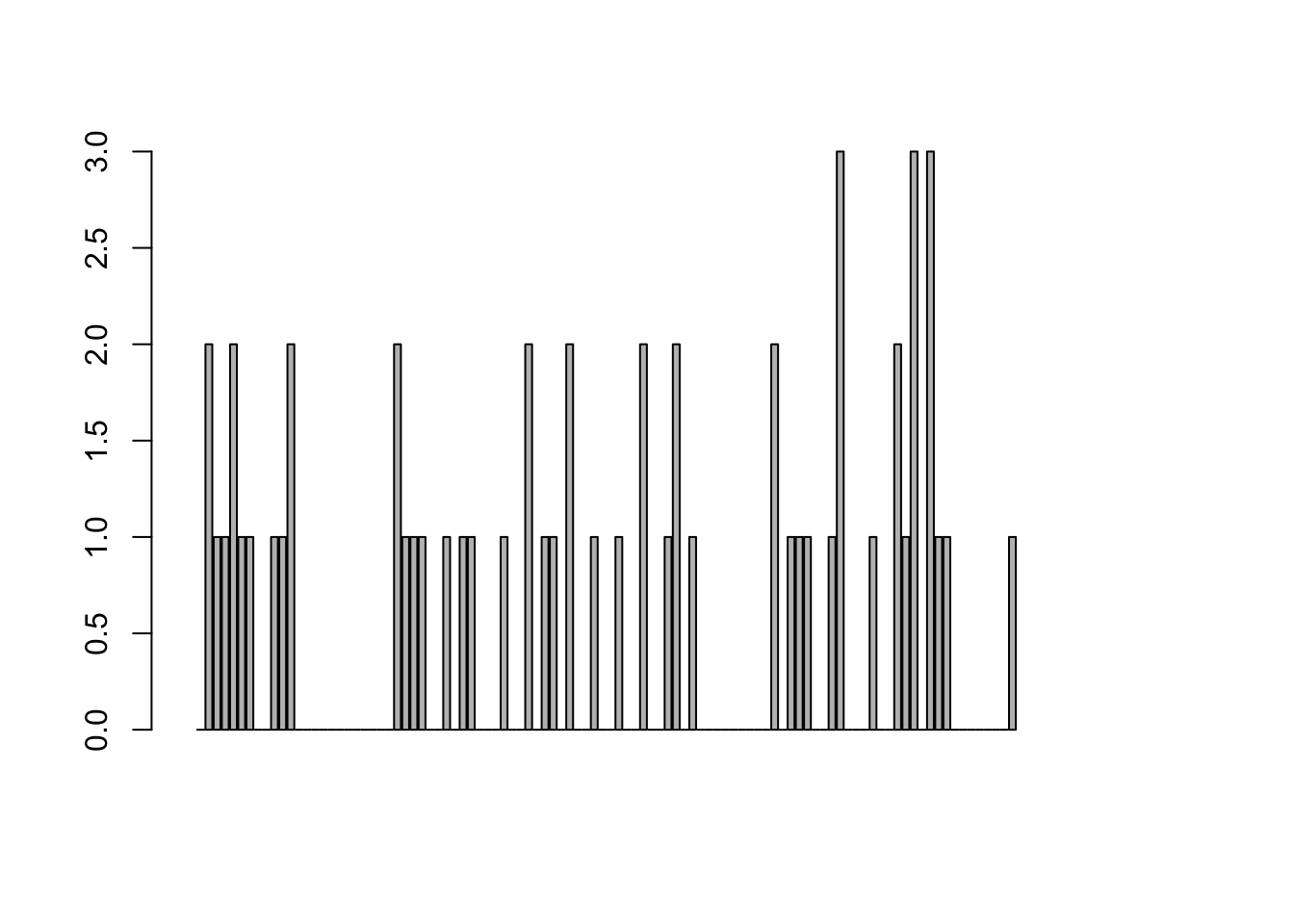
如果个别位点特别容易检测到表位,那肯定就不符合泊松分布了,需要进行计算分析。载入书中所给数据。
## [1] 2 0 1 0 0 0 2 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 0 0 0 1 0 0 0 0 1 0
## [36] 1 1 0 1 2 2 7 1 0 2 0 1 0 1 1 1 1 0 1 0 0 0 0 1 2 2 1 0 0 0 0 0 1 0 0
## [71] 0 1 1 0 0 1 1 0 0 0 0 1 0 0 0 1 0 1 0 0 1 1 0 0 1 1 0 0 1 0barplot(e100, ylim = c(0, 7), width = 0.7, xlim = c(-0.5, 100.5),
names.arg = seq(along = e100), col = "darkolivegreen")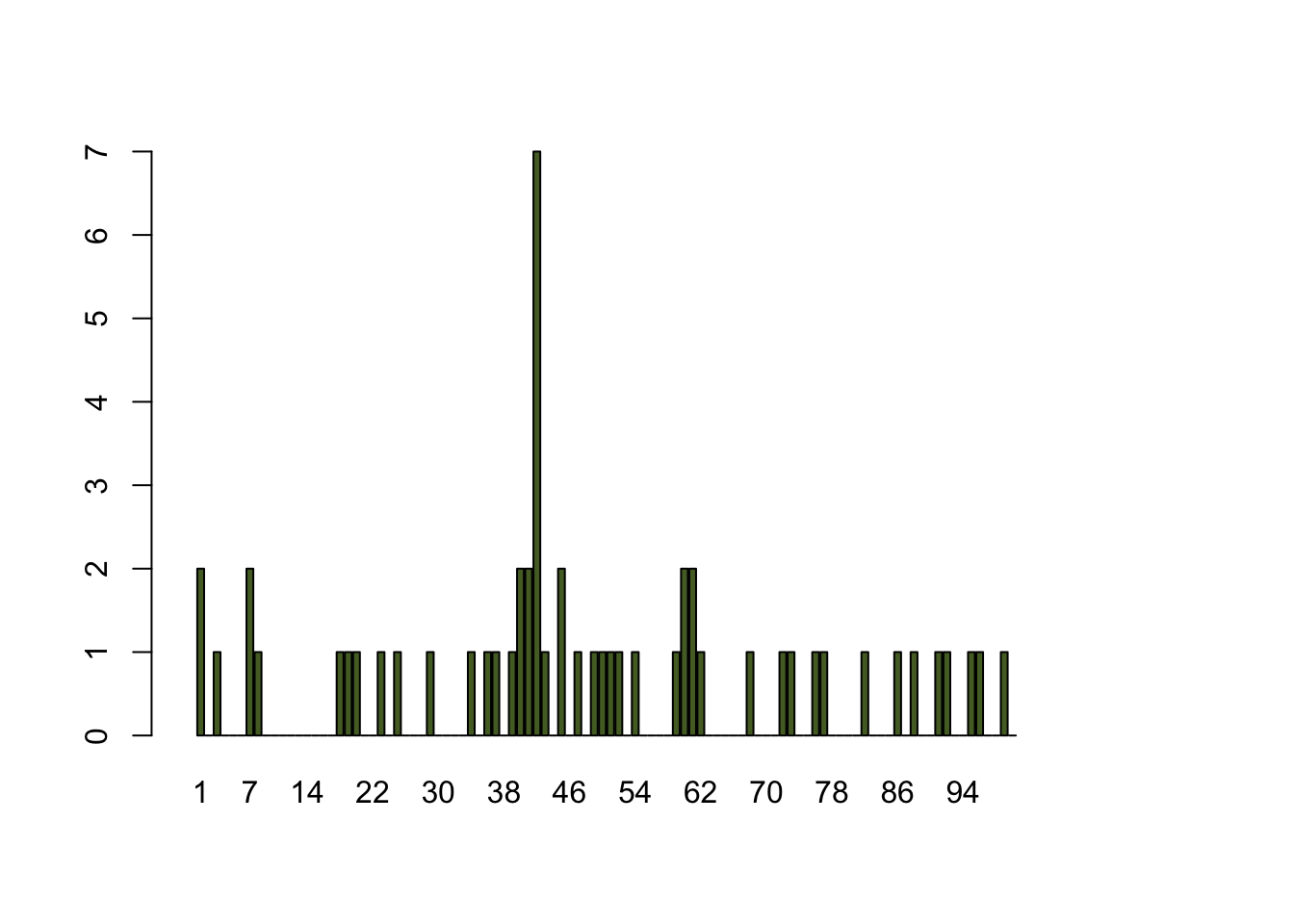
一看,有点不正常,50个人里居然有7个在某位点检测到表位,这符合泊松分布吗?这就是计算平均值为0.5的时候,密度为7的概率。我的第一反应是这样算:
## [1] 9.401827e-07但书中绕了个圈,不但没说这么算, 也不对,应该计算100个的泊松分布中,最大值大于等于7的概率。这就是,也就是。注意这个epsilon在数学里经常用来表示一个很小的数。经过 ,或者用模拟(simulation)算,这里用的蒙特拉罗方法(Monte Carlo method)。
## maxes
## 1 2 3 4 5 6 7 8
## 9 23710 60413 14201 1518 135 13 1这里面大于等于7的个数,除以10000,就是用模拟算出来的,符合泊松分布出现大于等于7的概率。
## [1] 0.00014可以看到,和我想的方法相比,虽然都很小,但是有数量级的差别。至于为什么先存疑。另外,用模拟的方法计算,精度受到模拟次数的限制。这很好理解,比如做10000次模拟,只能除以10000,没法达到更小的数位,所以不能得到0.00000000123这样的结果。
2.8 多项分布(Multinomial distribution)
当一次试验有大于2个结果时,就要引入多项分布。同样,一次试验的多个结果要有互斥、加和为1等特点。如一种产品分成几种等级,一段基因有4种碱基等情况。

Figure 2.10: 多项式模型
原书中在推导了多项分布的公式后,提出一个问题:球落到4个盒子之一的问题,如果落到各盒子的几率相等,那么观察到4个球落到第一个盒子,2个球落到第二个盒子,其他两个没有的概率是多少。
## [1] 0.0036621092.9 多项分布的权重(power)
这一部分没看太明白,先放着,往后看。
主要涉及解决“需要多大样本量”的问题。通过蒙特拉罗方法,确定我们需要多大的样本量,才能检验概率相等一个多项分布模型,是否与实际数据一致。
)](static/Users/eco/M%20for%20M/01-generative_files/dna.jpg)